1. Download Fortect and install it on your computer
2. Launch the program and click "Scan"
3. Click "Repair" to fix any issues that are found
Speed up your computer's performance now with this simple download.
In this guide, we will identify some of the possible causes that can cause Standard Errors to be interpreted, and then I will provide possible repair methods with which you can try to resolve this issue. The standard error (“Std Err” or “SE”) is a measure of the reliability of the mean. A small SE indicates that the sample mean, in turn, is a much more accurate reflection of the actual multiple mean. A larger sample size is likely to generally result in a smaller SE (whereas SD is not directly related to the sample size).
The standard error tells you how closely the mean of another given sample from that population compares to the true mean of the crowd. As the standard error increases, i.e. H The more spread out the means are, the more likely it is that the program will consider this assumption to be an inaccurate representation of the corresponding population mean.
</p>
<div></p>
<div style="box-shadow: rgba(0, 0, 0, 0.18) 0px 2px 4px;padding:20px 10px 20px 10px;">
<p><h2 id="4"><span class="ez-toc-section" id="How_do_you_interpret_a_large_standard_error"></span>How do you interpret a large standard error?<span class="ez-toc-section-end"></span></h2>
<p>A high standard error indicates that many of the sample means are widely dispersed in the population mean. Your sample may not match your population. A low conditional error indicates that the sample means are close to the population mean—your sample is a proxy for your population.</p>
</div>
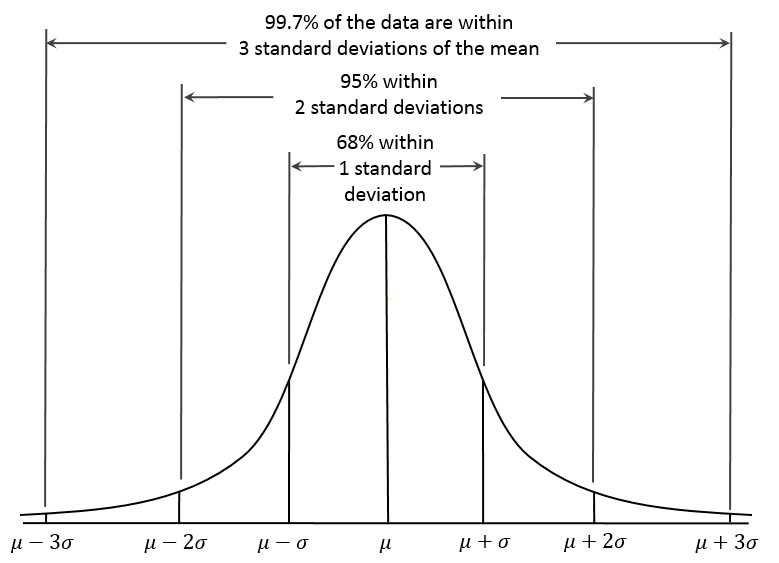
<p>Standard deviation and standard error are perhaps not just one but two of the least understood statistic Ticks usually displayed on history charts. The following article is intended to help you explain their meaning and provide more information about their use in a detailed analysis.</p>
<p><img decoding="async" src="/posts/interpreting-standard-error.jpg" style="margin-top:20px; margin-bottom:20px; width: 50%; height: auto; display: block; margin: 0 auto;" alt="interpreting standard error"></p>
<p>Standard deviation and standard error are probably two of the most misunderstood statistics that often appear in datasheets. The following article aims to explain their importance and provide more information on how to obtain them in data analysis. Both statistics are regularly displayed with an aspect average, and in a sense they both speak of an average. They are often referred to as “standard deviation of the mean” and “standard deviation of the underlying mean”. However, they are not interchangeable and also represent very different concepts.</p>
<p></p>
<div style="box-shadow: rgba(0, 0, 0, 0.18) 0px 2px 4px;padding:20px 10px 20px 10px;">
<p><h2 id="1"><span class="ez-toc-section" id="How_do_you_interpret_standard_error_in_statistics"></span>How do you interpret standard error in statistics?<span class="ez-toc-section-end"></span></h2>
<p>Standard error is the degree to which the mean of almost any given sample from that population can usually be compared to the true mean of the population. If the paradigm error increases, i.e. H. If the means are more varied, the likelihood increases that the mean is an inaccurate representation of the mean of the population of facts.</p>
</div>
<p>Standard deviation<br />The standard deviation (often abbreviated “Std Dev” or “SD”) measures how much a subject’s responses to a question vary or simply “deviate” from the mean. The SD tells the analyst how scattered the responses will be – are they grouped Are they around the middle, more scattered and wide? Did all your respondents rate your product in the middle of the scale, or did some like it and some dislike it?</p>
<p></p>
<div style="box-shadow: rgba(0, 0, 0, 0.18) 0px 2px 4px;padding:20px 10px 20px 10px;">
<p><h2 id="3"><span class="ez-toc-section" id="What_is_an_acceptable_standard_error"></span>What is an acceptable standard error?<span class="ez-toc-section-end"></span></h2>
<p>A score between 0.8 and 0.9 is considered by suppliers and regulators to be sufficient evidence of acceptable durability for any rating.</p>
</div>
<p>Let’s say you asked respondents to rate your course on a number of attributes on their 5-point scale. The mean for a group of ten respondents (denoted “A” in “J” below) for “value for money” was 3.2 with a standard deviation of 0.4, while the mean for “product reliability” was actually 3.4a with standard deviation. 2.1. . At first glance (just looking at the methods) it seems that reliability has been valued over value. But a higher standard deviation for reliability may indicate (as shown in the distribution below) that responses were relatively polarized, with the majority of respondents having no consistency issues (score with attribute “5”), and a smaller but important segment of responses . participants encountered a reliability issue and rated our own attribute as “1”. Looking at the mean by itself only tells part of the story, so far detectivesyou often focus on that as well. The distribution of responses is certainly an important factor, and SD promises a valuable description of this indicator.</p>
<table readabilitydatatable="1"><body></p>
<tr>
<td>Respondent:</td>
<td>Good value for money<br />for money:</td>
<td>Product<br />Reliability:</td>
</tr>
<tr>
<td>A</td>
<td>3</td>
<td>1</td>
</tr>
<tr>
<td>B</td>
<td>3</td>
<td>1</td>
</tr>
<tr>
<td>S</td>
<td>3</td>
<td>1</td>
</tr>
<tr>
<td>D</td>
<td>3</td>
<td>1</td>
</tr>
<tr>
<td>E</td>
<td>4</td>
<td>5</td>
</tr>
<tr>
<td>F</td>
<td>4</td>
<td>5</td>
</tr>
<tr>
<td>G</td>
<td>3</td>
<td>5</td>
</tr>
<tr>
<td>N</td>
<td>3</td>
<td>5</td>
</tr>
<tr>
<td>Me</td>
<td>3</td>
<td>5</td>
</tr>
<tr>
<td>J</td>
<td>3</td>
<td>5</td>
</tr>
<tr>
<td>Average</td>
<td>3.2</td>
<td>3.4</td>
</tr>
<tr>
<td>Standard development</td>
<td>0.4</td>
<td>2.1</td>
</tr>
</tbody>
</table>
<div style="background: rgba(156, 156, 156, 0.07);margin:20px 0 20px 0;padding:20px 10px 20px 10px;border: solid 1px rgba(0,0,0,0.03);text-align: left;"><h2><span class="ez-toc-section" id="Approved_Fortect-2"></span>Approved: <a href="https://www.fortect.com/go/route-wki.php?channel=wki&d=t&adgroup=windowsdiary.com" target="_blank" rel="nofollow">Fortect</a><span class="ez-toc-section-end"></span></h2>
<p><a href="https://www.fortect.com/go/route-wki.php?channel=wki&d=t&adgroup=windowsdiary.com" target="_blank" rel="nofollow">Fortect</a> is the world's most popular and effective PC repair tool. It is trusted by millions of people to keep their systems running fast, smooth, and error-free. With its simple user interface and powerful scanning engine, <a href="https://www.fortect.com/go/route-wki.php?channel=wki&d=t&adgroup=windowsdiary.com" target="_blank" rel="nofollow">Fortect</a> quickly finds and fixes a broad range of Windows problems - from system instability and security issues to memory management and performance bottlenecks.</p>
<li>1. Download <a href="https://www.fortect.com/go/route-wki.php?channel=wki&d=t&adgroup=windowsdiary.com" target="_blank" rel="nofollow">Fortect</a> and install it on your computer</li>
<li>2. Launch the program and click "Scan"</li>
<li>3. Click "Repair" to fix any issues that are found</li>
<br><a href="https://www.fortect.com/go/route-wki.php?channel=wki&d=t&adgroup=windowsdiary.com" target="_blank" rel="nofollow" alt="download"><img src="/wp-content/download3.png" style="width:340px;"></a></div>
<p>Two very different deductions in response to a 5-point increase can result in the same average. Consider the following example, which shows the response to values with different scores. In the first representation (note the “a”) the standard deviation is zero because ALL of the responses were exactly love. Individual responses do not deviate from the mean. When assessing ” ” the group standard deviation is higher even if the group is equal to the first distribution (3rd As 0). A standard deviation of 1.15 indicates that, on average*, the individual response was slightly different from the average by at least one point.</p>
<table readabilitydatatable="1"><body></p>
<tr>
<td>Respondent:</td>
<td>Rating “A”</td>
<td>Class “B”</td>
</tr>
<tr>
<td>A</td>
<td>3</td>
<td>1</td>
</tr>
<tr>
<td>B</td>
<td>3</td>
<td>2</td>
</tr>
<tr>
<td>S</td>
<td>3</td>
<td>2</td>
</tr>
<tr>
<td>D</td>
<td>3</td>
<td>3</td>
</tr>
<tr>
<td>E</td>
<td>3</td>
<td>3</td>
</tr>
<tr>
<td>F</td>
<td>3</td>
<td>3</td>
</tr>
<tr>
<td>G</td>
<td>3</td>
<td>3</td>
</tr>
<tr>
<td>N</td>
<td>3</td>
<td>4</td>
</tr>
<tr>
<td>Me</td>
<td>3</td>
<td>4</td>
</tr>
<tr>
<td>J</td>
<td>3</td>
<td>5</td>
</tr>
<tr>
<td>Average</td>
<td>3.0</td>
<td>3.0</td>
</tr>
<tr>
<td>Standard development</td>
<td>0.00</td>
<td>1.15</td>
</tr>
</tbody>
</table>
<p><img decoding="async" src="https://i.ytimg.com/vi/T2gCe1O7xi8/maxresdefault.jpg" style="margin-top:20px; margin-bottom:20px; display: block; margin: 0 auto;" alt="interpreting standard error"></p>
<p>Another way to look at standard deviation is to represent the distribution as a histogram of responses. A distribution based on a low standard deviation will look like the last tall narrow figure, while a distribution based on a large standard deviation will look like the tallest figure.</p>
<p>Standard deviation does not usually mean “true and/or possibly false” or “better or worse”. Heused only as a descriptive statistic. Describes the distribution relative to the mean.</p>
<p>*Technical disclaimer. Thinking of the standard deviation as the “mean deviation” is in some ways helpful in understanding your message conceptually. However, it doesn’t actually calculate the mean (if it did, we could call it “mean deviation”). Instead, it’s a “standardized”, somewhat complicated method where the value is calculated using the sum associated with the squares. For practical reasons, elaboration is not important. Most spreadsheet programs, Excel spreadsheets, or other data management tools will determine the SD for you. To understand what the report says, it is very important to know more.</p>
<p></p>
<div style="box-shadow: rgba(0, 0, 0, 0.18) 0px 2px 4px;padding:20px 10px 20px 10px;">
<p><h2 id="2"><span class="ez-toc-section" id="What_is_a_good_level_of_standard_error"></span>What is a good level of standard error?<span class="ez-toc-section-end"></span></h2>
<p>With an eigenvalue of 95%, 95% of all inclusions in a sample are expected to correspond to a confidence interval of ± 1.96 sample base errors. Random samples are also used to estimate the actual population parameter that falls within this range, with a 95% confidence level.</p>
</div>
</p>
<a href="https://www.fortect.com/go/route-wki.php?channel=wki&d=t&adgroup=windowsdiary.com" target="_blank" rel="nofollow"> Speed up your computer's performance now with this simple download. </a>
</p>
<p><a href="https://windowsdiary.com/it/suggerimenti-per-la-risoluzione-dei-problemi-per-linterpretazione-degli-errori-standard/" class="translate" hreflang="it"><img decoding="async" src="/wp-includes/images/flags/it.png" width="40" height="30"></a> <a href="https://windowsdiary.com/pl/wskazowki-dotyczace-rozwiazywania-problemow-dotyczacych-interpretacji-bledow-standardowych/" class="translate" hreflang="pl"><img decoding="async" src="/wp-includes/images/flags/pl.png" width="40" height="30"></a> <a href="https://windowsdiary.com/nl/tips-voor-het-oplossen-van-problemen-voor-het-interpreteren-van-standaardfouten/" class="translate" hreflang="nl"><img decoding="async" loading="lazy" src="/wp-includes/images/flags/nl.png" width="40" height="30"></a> <a href="https://windowsdiary.com/sv/felsokningstips-angaende-tolkning-av-standardfel/" class="translate" hreflang="sv"><img decoding="async" loading="lazy" src="/wp-includes/images/flags/sv.png" width="40" height="30"></a> <a href="https://windowsdiary.com/ko/%ed%91%9c%ec%a4%80-%ec%98%a4%eb%a5%98-%ed%95%b4%ec%84%9d%ec%9d%84-%ec%9c%84%ed%95%9c-%eb%ac%b8%ec%a0%9c-%ed%95%b4%ea%b2%b0-%ed%8c%81/" class="translate" hreflang="ko"><img decoding="async" loading="lazy" src="/wp-includes/images/flags/ko.png" width="40" height="30"></a> <a href="https://windowsdiary.com/de/tipps-zur-fehlerbehebung-bei-der-interpretation-von-standardfehlern/" class="translate" hreflang="de"><img decoding="async" loading="lazy" src="/wp-includes/images/flags/de.png" width="40" height="30"></a> <a href="https://windowsdiary.com/pt/dicas-de-solucao-de-problemas-para-interpretar-erros-padrao/" class="translate" hreflang="pt"><img decoding="async" loading="lazy" src="/wp-includes/images/flags/pt.png" width="40" height="30"></a></p>
<div class="saboxplugin-wrap" itemtype="http://schema.org/Person" itemscope itemprop="author"><div class="saboxplugin-tab"><div class="saboxplugin-gravatar"><img decoding="async" loading="lazy" src="https://windowsdiary.com/wp-content/uploads/kaimitchell.jpg" width="100" height="100" alt="Kai Mitchell" itemprop="image"></div><div class="saboxplugin-authorname"><a href="https://windowsdiary.com/author/kaimitchell/" class="vcard author" rel="author"><span class="fn">Kai Mitchell</span></a></div><div class="saboxplugin-desc"><div itemprop="description"></div></div><div class="clearfix"></div></div></div><div class="crp_related crp-rounded-thumbs"><h3>Related Posts:</h3><ul><li><a href="https://windowsdiary.com/en/microsoft-word-connecting-to-printer-error/" class="crp_link post-195650"><figure><img loading="lazy" width="150" height="150" src="https://windowsdiary.com/wp-content/uploads/2022/04/microsoft-word-connecting-to-printer-error-150x150.jpg" class="crp_featured crp_thumb crp_thumbnail" alt="microsoft-word-connecting-to-printer-error" title="Tips For Resolving Microsoft Word Connection Errors With Printer Errors" /></figure><span class="crp_title">Tips For Resolving Microsoft Word Connection Errors…</span></a></li><li><a href="https://windowsdiary.com/en/network-error-dns-server-failure/" class="crp_link post-200838"><figure><img loading="lazy" width="150" height="150" src="https://windowsdiary.com/wp-content/uploads/2022/04/network-error-dns-server-failure-150x150.png" class="crp_featured crp_thumb crp_thumbnail" alt="network-error-dns-server-failure" title="Tips For Fixing Network Errors, DNS Server Errors" /></figure><span class="crp_title">Tips For Fixing Network Errors, DNS Server Errors</span></a></li><li><a href="https://windowsdiary.com/en/standard-error-of-the-sample-means-calculator/" class="crp_link post-202741"><figure><img loading="lazy" width="150" height="150" src="https://windowsdiary.com/wp-content/uploads/2022/04/standard-error-of-the-sample-means-calculator-150x150.png" class="crp_featured crp_thumb crp_thumbnail" alt="standard-error-of-the-sample-means-calculator" title="Tips For Correcting The Standard Error Of The Sample Mean Calculator" /></figure><span class="crp_title">Tips For Correcting The Standard Error Of The Sample…</span></a></li><li><a href="https://windowsdiary.com/en/how-to-remove-script-error-virus/" class="crp_link post-142145"><figure><img loading="lazy" width="150" height="150" src="https://windowsdiary.com/wp-content/uploads/2021/12/how-to-remove-script-error-virus-150x150.jpg" class="crp_featured crp_thumb crp_thumbnail" alt="how-to-remove-script-error-virus" title="Troubleshooting Tips For Script Virus Errors" /></figure><span class="crp_title">Troubleshooting Tips For Script Virus Errors</span></a></li><li><a href="https://windowsdiary.com/en/application-error-the-instruction-at/" class="crp_link post-128074"><figure><img loading="lazy" width="150" height="150" src="https://windowsdiary.com/wp-content/uploads/2021/12/application-error-the-instruction-at-150x150.png" class="crp_featured crp_thumb crp_thumbnail" alt="application-error-the-instruction-at" title="For Tips On Troubleshooting Application Errors, See The Instructions On" /></figure><span class="crp_title">For Tips On Troubleshooting Application Errors, See…</span></a></li><li><a href="https://windowsdiary.com/en/troubleshoot-cisco-switch-ports/" class="crp_link post-195690"><figure><img loading="lazy" width="150" height="150" src="https://windowsdiary.com/wp-content/uploads/2022/04/troubleshoot-cisco-switch-ports-150x150.jpg" class="crp_featured crp_thumb crp_thumbnail" alt="troubleshoot-cisco-switch-ports" title="Tips For Troubleshooting Cisco Switch Port Errors" /></figure><span class="crp_title">Tips For Troubleshooting Cisco Switch Port Errors</span></a></li></ul><div class="crp_clear"></div></div>
</div><!-- .entry-content -->
</article><!-- #post-173308 -->
</main><!-- #main -->
</div><!-- #primary -->
<aside id="secondary" class="featured-sidebar widget-area">
<section id="search-2" class="fbox swidgets-wrap widget widget_search"><form role="search" method="get" class="search-form" action="https://windowsdiary.com/">
<label>
<span class="screen-reader-text">Search for:</span>
<input type="search" class="search-field" placeholder="Search …" value="" name="s" />
</label>
<input type="submit" class="search-submit" value="Search" />
</form></section>
<section id="recent-posts-2" class="fbox swidgets-wrap widget widget_recent_entries">
<div class="swidget"><div class="sidebar-title-border"><h3 class="widget-title">Recent Posts</h3></div></div>
<ul>
<li>
<a href="https://windowsdiary.com/pt/resolvendo-seu-erro-atual-do-steam-voce-nao-tem-espaco-suficiente-em-disco/">Resolvendo Seu Erro Atual Do Steam, Você Não Tem Espaço Suficiente Em Disco</a>
</li>
<li>
<a href="https://windowsdiary.com/sv/pci-kompatibelt-antivirusfelsokningstips/">PCI-kompatibelt Antivirusfelsökningstips</a>
</li>
<li>
<a href="https://windowsdiary.com/nl/stappen-om-geheugenlekken-in-backend-weergaven-op-te-lossen/">Stappen Om Geheugenlekken In Backend-weergaven Op Te Lossen</a>
</li>
<li>
<a href="https://windowsdiary.com/nl/stappen-die-itunes-repareren-in-de-veilige-modus-op-mac/">Stappen Die ITunes Repareren In De Veilige Modus Op Mac</a>
</li>
<li>
<a href="https://windowsdiary.com/ko/photoshop-cs4%eb%a5%bc-%ec%84%a4%ec%b9%98%ed%95%a0-%eb%95%8c-%ec%98%a4%eb%a5%98-1603%ec%9d%84-%ec%88%98%ec%a0%95%ed%95%98%eb%8a%94-%eb%b0%a9%eb%b2%95%ec%9d%80-%eb%ac%b4%ec%97%87%ec%9e%85%eb%8b%88/">Photoshop CS4를 설치할 때 오류 1603을 수정하는 방법은 무엇입니까?</a>
</li>
</ul>
</section></aside><!-- #secondary -->
</div>
</div><!-- #content -->
</div>
<footer id="colophon" class="site-footer clearfix">
<div class="content-wrap">
</div>
<div class="site-info">
©2024 Windows Diary <!-- Delete below lines to remove copyright from footer -->
<span class="footer-info-right">
| Built using WordPress and <a href="https://superbthemes.com/responsiveblogily/">Responsive Blogily</a> theme by Superb
</span>
<!-- Delete above lines to remove copyright from footer -->
</div><!-- .site-info -->
</div>
</footer><!-- #colophon -->
</div><!-- #page -->
<div id="smobile-menu" class="mobile-only"></div>
<div id="mobile-menu-overlay"></div>
<!-- Start of StatCounter Code -->
<script>
<!--
var sc_project=12585252;
var sc_security="fad14f33";
var sc_invisible=1;
var scJsHost = (("https:" == document.location.protocol) ?
"https://secure." : "http://www.");
//-->
</script>
<script type="text/javascript"
src="https://secure.statcounter.com/counter/counter.js"
async></script> <noscript><div class="statcounter"><a title="web analytics" href="https://statcounter.com/"><img class="statcounter" src="https://c.statcounter.com/12585252/0/fad14f33/1/" alt="web analytics" /></a></div></noscript>
<!-- End of StatCounter Code -->
<script type='text/javascript' id='ez-toc-scroll-scriptjs-js-extra'>
/* <![CDATA[ */
var eztoc_smooth_local = {"scroll_offset":"30","add_request_uri":""};
/* ]]> */
</script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/plugins/easy-table-of-contents/assets/js/smooth_scroll.min.js?ver=2.0.69.1' id='ez-toc-scroll-scriptjs-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/plugins/easy-table-of-contents/vendor/js-cookie/js.cookie.min.js?ver=2.2.1' id='ez-toc-js-cookie-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/plugins/easy-table-of-contents/vendor/sticky-kit/jquery.sticky-kit.min.js?ver=1.9.2' id='ez-toc-jquery-sticky-kit-js'></script>
<script type='text/javascript' id='ez-toc-js-js-extra'>
/* <![CDATA[ */
var ezTOC = {"smooth_scroll":"1","visibility_hide_by_default":"1","scroll_offset":"30","fallbackIcon":"<span class=\"\"><span class=\"eztoc-hide\" style=\"display:none;\">Toggle<\/span><span class=\"ez-toc-icon-toggle-span\"><svg style=\"fill: #999;color:#999\" xmlns=\"http:\/\/www.w3.org\/2000\/svg\" class=\"list-377408\" width=\"20px\" height=\"20px\" viewBox=\"0 0 24 24\" fill=\"none\"><path d=\"M6 6H4v2h2V6zm14 0H8v2h12V6zM4 11h2v2H4v-2zm16 0H8v2h12v-2zM4 16h2v2H4v-2zm16 0H8v2h12v-2z\" fill=\"currentColor\"><\/path><\/svg><svg style=\"fill: #999;color:#999\" class=\"arrow-unsorted-368013\" xmlns=\"http:\/\/www.w3.org\/2000\/svg\" width=\"10px\" height=\"10px\" viewBox=\"0 0 24 24\" version=\"1.2\" baseProfile=\"tiny\"><path d=\"M18.2 9.3l-6.2-6.3-6.2 6.3c-.2.2-.3.4-.3.7s.1.5.3.7c.2.2.4.3.7.3h11c.3 0 .5-.1.7-.3.2-.2.3-.5.3-.7s-.1-.5-.3-.7zM5.8 14.7l6.2 6.3 6.2-6.3c.2-.2.3-.5.3-.7s-.1-.5-.3-.7c-.2-.2-.4-.3-.7-.3h-11c-.3 0-.5.1-.7.3-.2.2-.3.5-.3.7s.1.5.3.7z\"\/><\/svg><\/span><\/span>","chamomile_theme_is_on":""};
/* ]]> */
</script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/plugins/easy-table-of-contents/assets/js/front.min.js?ver=2.0.69.1-1729222029' id='ez-toc-js-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/themes/responsiveblogily/js/navigation.js?ver=20170823' id='responsiveblogily-navigation-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/themes/responsiveblogily/js/skip-link-focus-fix.js?ver=20170823' id='responsiveblogily-skip-link-focus-fix-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/themes/responsiveblogily/js/script.js?ver=20160720' id='responsiveblogily-script-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/themes/responsiveblogily/js/jquery.flexslider.js?ver=20150423' id='responsiveblogily-flexslider-js'></script>
<script type='text/javascript' src='https://windowsdiary.com/wp-content/themes/responsiveblogily/js/accessibility.js?ver=20160720' id='responsiveblogily-accessibility-js'></script>
<script>
/(trident|msie)/i.test(navigator.userAgent)&&document.getElementById&&window.addEventListener&&window.addEventListener("hashchange",function(){var t,e=location.hash.substring(1);/^[A-z0-9_-]+$/.test(e)&&(t=document.getElementById(e))&&(/^(?:a|select|input|button|textarea)$/i.test(t.tagName)||(t.tabIndex=-1),t.focus())},!1);
</script>
</body>
</html>
