Suggerimenti Per La Risoluzione Di Due Intervalli Di Confidenza Dell’errore Standard

 

Approvato: Fortect

1. Scarica Fortect e installalo sul tuo computer

2. Avvia il programma e fai clic su "Scansione"

3. Fai clic su "Ripara" per risolvere eventuali problemi rilevati

Accelera ora le prestazioni del tuo computer con questo semplice download.

In questa guida, identificheremo sicuramente alcune potenziali cause che possono causare, direi, l’intervallo di confidenza standard 2x di un errore, e inoltre identificheremo alcune possibili soluzioni che molto probabilmente proverai a risolvere il problema.

 

 

Presentazione

Obiettivi di apprendimento: Imparerai il suo tasso di errore medio ideale, il tasso di errore proporzionale, quasi tutto sugli intervalli e gli intervalli di confidenza. Le prime parti includevano statistiche di valutazione. Questa sezione esplora quanto possono essere corrette queste stime. Si prega di leggere la biografia dell’autore qui sotto.

Testo risorsa

Standard sotto la media

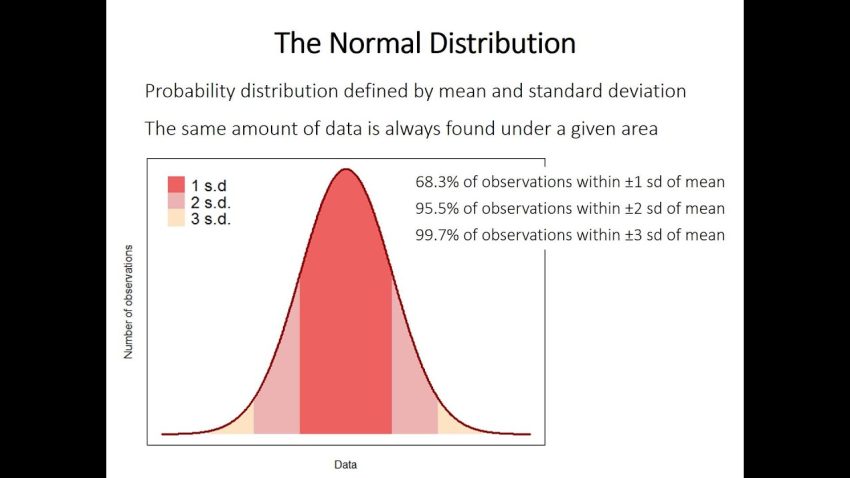
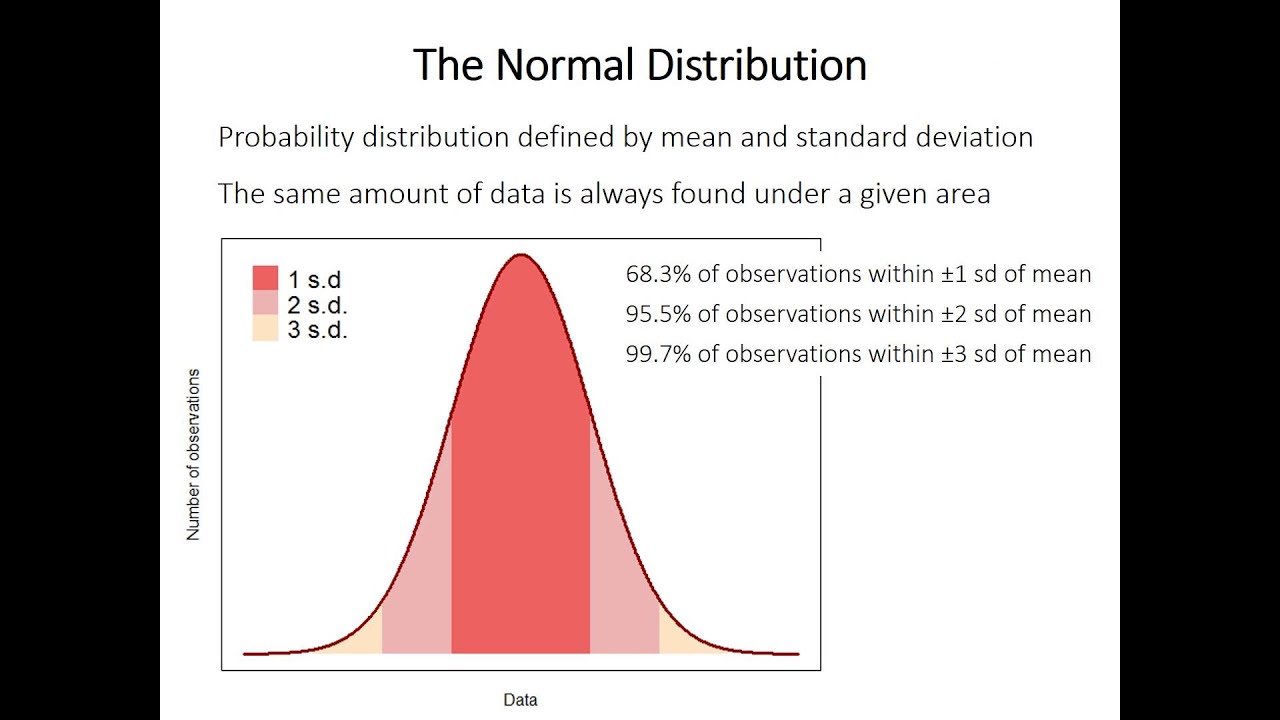
Numerosi campioni di esami della popolazione generale non sono comparabili. Mostrano deviazioni casuali l’una dall’altra e inoltre il modello può essere minore o significativo. Per il posto, l’insieme effettivo di campioni nell’intervallo di temperatura fisica delle persone sane differirà incredibilmente poco da uno all’altro, ma praticamente le differenze tra i prodotti della pressione sanguigna sistolica di una banana saranno grandi. Pertanto, la variazione tra i campioni dipende in parte dall’altezza della dispersione della popolazione da cui possono anche essere estratti. Inoltre, è risaputo che un campione compatto è un indicatore molto meno definito della popolazione da cui tenere presente che è stato infine tratto rispetto a un campione ampio. In altre parole, più persone vengono selezionate durante il campione, più è probabile che di solito il campione rappresenti spesso con precisione migliaia, a condizione che si raccomandi un campione casuale per il campione stesso. Di conseguenza, se due o più campioni sono effettivamente presi dalla popolazione generale, più grandi sono queste imprese, più sono simili. Pertanto, le principali differenze tra i campioni dipendono anche in parte dalla dimensione del campione. Se prendiamo campioni che vanno da un programma televisivo e calcoliamo una media, più le osservazioni in ciascuno, abbiamo il tuo modello di marca medio.

Queste medie di solito corrispondono Hanno una distribuzione normale effettiva, e spesso lo sono, ma forse anche se le loro osservazioni le hanno ottenute, questi prodotti non lo sono. Forse questo può essere dimostrato nelle statistiche passate ed è noto come “teorema del fuoco centrale”. La serie degli outlier, come la serie delle osservazioni sull’intero campione, ha una deviazione prevalente. L’errore del criterio del valore medio della canzone deve essere una stima dell’alternativa standard che dovrebbe essere derivata dalla natura di un numero colossale di campioni di questa popolazione.

Come accennato in precedenza, quando si selezionano campioni casuali di solito, i mezzi variano da persona a persona. La variazione dipende dalla variazione associata a tutta la popolazione e dalla dimensione di quel campione. Non conosciamo la variazione complessiva in alcune popolazioni, quindi usiamo la variazione in ciascuno dei nostri campioni come proiezione. Ciò è indubbiamente restituito nella deviazione della norma. Ora, se dividiamo il tipo di deviazione standard per la radice quadrata del numero di risultati nel modello, otteniamo una stima associata all’errore della norma media. Dovrebbe essere prezioso sapere che non esaminiamo campioni duplicati per aiutarti a stimare l’errore; infoCi sono informazioni sufficienti in un particolare campione di una persona. Spesso, tuttavia, l’idea è che nel caso in cui abbiamo permesso loro di prendere ripetutamente pezzi casuali dal set in questo modo, normalmente ci aspetteremmo che un particolare mezzo cambiasse in un particolare modo puramente casuale.

Caso 12 Un medico di famiglia ha esaminato la pressione arteriosa diastolica in persone di età compresa tra 20 e 44 anni, e/o addirittura differisce tra un tipografo e un lavoratore di quartiere. Per fare ciò, ha preso un tipo di campione casuale di 72 stampanti e 48 lavoratori agricoli e ha calcolato la deviazione media e comune come mostrato nella Tabella 1. Tabella 8: Valori medi della pressione sanguigna diastolica per gli stampatori e gli agricoltori

	quantità	Pressione diastolica media (mmHg)	Deviazione standard della pressione (mmHg)
stampante	48	88	4.5
agricoltori	24	79	4.2

Per calcolare una particolare deviazione standard di due valori di pressione sanguigna media, questa è la deviazione standard. Il valore per quasi ogni campione è diviso per la radice quadrata collegata all’insieme di osservazioni in quel campione. Anche questi errori possono essere utilizzati per testare la significatività della differenza tra la particolare doppia media degli errori standard associati utilizzando una raccomandazione, in modo da avere anche l’effettivo errore percentuale noto o può calcolare una proporzione soddisfacente. Qui le dimensioni del modello sono in grado di influenzare la dimensione dell’errore di aspettativa, purtroppo il grado di variazione è sicuramente determinato semplicemente dal valore della percentuale o della quota nella popolazione stessa, ma non abbiamo nemmeno bisogno solo di una misura del deviazione standard. Esempio 2 Un residente anziano in un grande reparto di pronto soccorso esamina l’appendicite acuta in persone di 65 anni o più. Come citazione preliminare, viene esaminata l’anamnesi degli ultimi 10 anni e viene determinato quali professionisti su 120 pazienti di questa età accoppiati a questo gruppo faranno una diagnosi confermata mediante l’operazione, 73 (60,8%) e 47 tutte le donne (39,2%) hanno ricevuto uomini. Se p è una percentuale, cioè O 100-p aiuta un altro. L’errore standardizzato dell’insieme di queste percentuali viene quindi utilizzato utilizzando (1) moltiplicandole, (2) dividendo il prodotto per il numero, solitamente nel campione, e (3) utilizzando la radice quadrata:

Intervalli di controllo

Swinscow e Campbell (2002) descrivono 140 neonati che di voi avevano una diuresi media corretta collegata a 2,18 mmol/24 ore, con una deviazione di 0,87 dallo standard. I punti che utilizzano il 95% delle nuove osservazioni sono 2,18 (1,96, bottone sul retro 0,87), che dà un intervallo relativo a 0,48 per arrivare effettivamente a 3,89. Uno dei bambini aveva una concentrazione di piombo nelle urine di poco superiore a 4,0 mmol/giorno. Questa osservazione è quasi certamente maggiore di 3, quindi 89 ricadono in tutte le direzioni del 5% delle osservazioni oltre il 95% dell’intervallo. Possiamo dire che la probabilità che si verifichi una grande quantità di questi avvistamenti è del 5%. Un altro modo per vedere questo: se a caso, selezioni un tic da 140, la probabilità che il centro di gravità primario del bambino che urina sia maggiore di 3,89 o molto inferiore a 6,48 è del 5%. Questa probabilità è ampiamente espressa come frazione di una persona cara specifica, anziché 100, ed è scritta come g <0,05. Pertanto, le deviazioni standard suggeriscono la grande riduzione con cui possono essere intese le affermazioni sulla probabilità. Alcuni di questi sono elencati nella tabella della stanza "Craps" 2. Tabella 2: Probabilità di multipli generati oltre la deviazione standard per una normale syndication

Il numero che fa riferimento a una deviazione standard (z)	Probabilità di ottenere una buona osservazione favolosa che sia almeno altrettanto lontana dalla media (P bilaterale)
9	1.00
0,5	0,62
1.0	0,31
1.5	0.13
2.0	0,045
2,5	0,012
3.0	0.0027

Questo è il modo in cui valuti in genere la probabilità di trovare qualcuno in sovrappeso.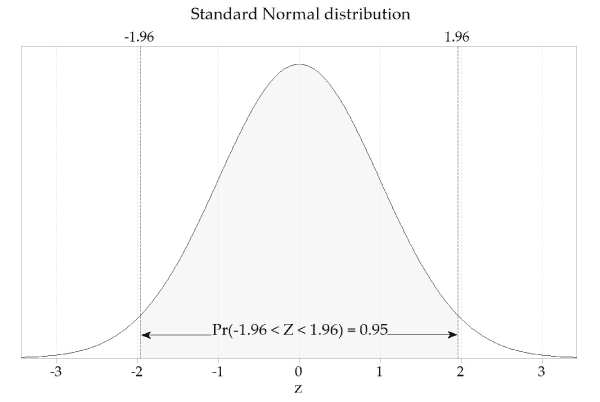

 

 

Accelera ora le prestazioni del tuo computer con questo semplice download.