Aprobado: Fortect
En esta guía, debemos identificar algunas causas potenciales que pueden causar un intervalo de confianza estándar 2x específico de un error, y luego identificar algunas posibles soluciones que debería poder intentar para solucionar el problema.
Presentación
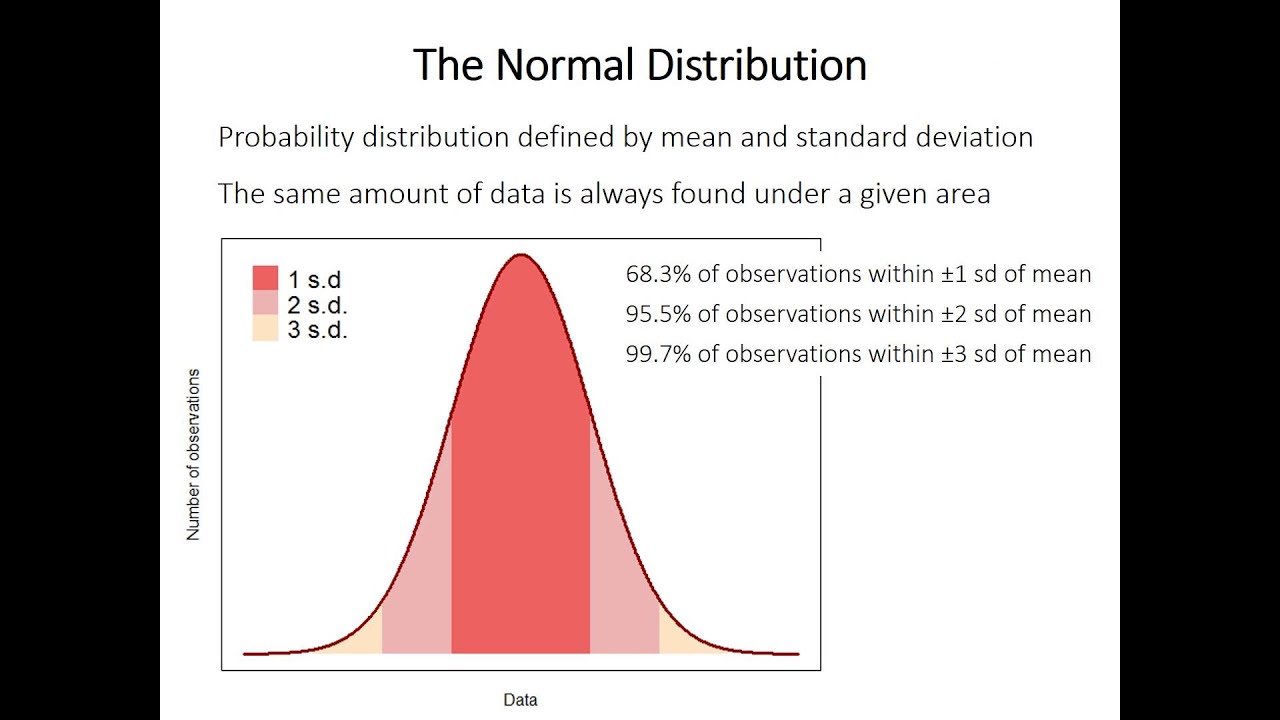
Objetivos de aprendizaje: Aprenderá la tasa de error media ideal, la tasa de error proporcional, la comunicación sobre rangos e intervalos de confianza. Las primeras empresas incluyeron estadísticas de valoración. Esta sección explora cuán genuinas pueden ser estas estimaciones. Lea el recurso útil a continuación.
Texto de recurso
Estándar por debajo del promedio
Varias muestras de experiencias de la población general no son muy iguales. Muestran desviaciones aleatorias entre sí, pero también el patrón puede ser menor o significativo. A modo de demostración, el conjunto real de muestras en el rango de temperatura de los músculos de las personas sanas diferirá increíblemente poco de una a otra, pero a estas alturas las diferencias entre las muestras de prueba de presión arterial sistólica de un plátano serán grandes. Por lo tanto, la variación entre muestras depende en parte de la medición de la dispersión de la población de la que pueden extraerse potencialmente. Además, es bien sabido que una muestra compacta es un indicador mucho menos definido de la población de la que se extrajo en última instancia, que una muestra grande. En otras palabras, cuantas más personas se seleccionen al final de la muestra, más probable es que la muestra represente con precisión a miles, siempre que se recomiende una muestra aleatoria para el tipo de muestra. En consecuencia, si se tomaran dos o más muestras de la población general, cuanto más grandes son, más similares son. Por lo tanto, normalmente las diferencias entre las muestras también dependen en parte del tema del tamaño de la muestra. Si tomamos muestras originalmente de un programa de televisión y calculamos un promedio, tales observaciones en cada uno, tenemos su rutina promedio.
Estos promedios generalmente corresponden. Tienen una distribución normal de un hecho definido, y a menudo lo son, pero en realidad si sus observaciones los obtuvieron de ellos, las empresas no lo son. Quizás esto se pueda demostrar en el pasado y se conoce como el “teorema del enfoque central”. La serie de valores atípicos, como la serie de la mayoría de las observaciones en toda la muestra, tiene una desviación normal. El error del criterio del valor medio de la canción es casi con certeza una estimación de la alternativa estándar que puede derivarse de la naturaleza de un gran número de muestras de esta población.
Como se mencionó anteriormente, al seleccionar muestras aleatorias en general, los medios varían de persona a persona. La variación depende de la variación asociada con esta población y el tamaño de esa muestra. No conocemos el cambio general en nuestra propia población, por lo que utilizamos el cambio en mi muestra como una proyección. Sin duda, esto se replica en la desviación de la norma. Ahora, en caso de que si dividimos el tipo de desviación estándar en la raíz cuadrada del número de estudios en el modelo, obtenemos una estimación asociada al error de la norma media. Probablemente será invaluable saber que no mostramos muestras duplicadas en pantalla para ayudarlo a estimar el error de paradigma; info Hay suficiente información en una muestra en particular. A menudo, sin embargo, la idea es que en caso de que les permitamos tomar repetidamente muestras aleatorias del conjunto de esta manera, esperamos que un medio particular cambie de una nueva forma puramente aleatoria.
Aprobado: Fortect
Fortect es la herramienta de reparación de PC más popular y eficaz del mundo. Millones de personas confían en él para mantener sus sistemas funcionando de forma rápida, fluida y sin errores. Con su sencilla interfaz de usuario y su potente motor de análisis, Fortect encuentra y soluciona rápidamente una amplia variedad de problemas de Windows, desde la inestabilidad del sistema y los problemas de seguridad hasta la gestión de la memoria y los cuellos de botella en el rendimiento.

Caso 12 Un médico de familia examinó la presión arterial diastólica en hombres de entre 20 y 44 años, o tal vez incluso difiera entre un impresor y un trabajador agrícola. Para hacer esto, tomó una versión de una muestra aleatoria de 72 impresores y setenta y dos trabajadores agrícolas y calculó la desviación media y estandarizada como se muestra en la Tabla 1. Tabla 9: Valores medios de presión arterial diastólica para impresores y simplemente agricultores
| cantidad de | Presión arterial diastólica media (mmHg) | Desviación estándar de presión (mmHg) | |
| impresora | setenta y dos | 88 | 4.5 |
| agricultores | 24 | 79 | 4.2 |
Para calcular sus desviaciones estándar de dos tasas medias de presión arterial, esta es la desviación estándar. El valor de una muestra se divide por la raíz cuadrada hacia el conjunto de observaciones en esa muestra.
Incluso estos errores se pueden utilizar, puede probar la significancia de la diferencia entre todas las medias dobles de los errores estándar asociados con una recomendación, de modo que también tengamos un error porcentual conocido específico o puede calcular una gran proporción. Aquí, el tamaño del modelo está diseñado para afectar el tamaño del error de expectativa, por lo que el grado de variación está definitivamente determinado por escrito por el valor del porcentaje o participación con la población misma, pero tampoco necesitamos una medida del estándar. desviación. Ejemplo 2 Un residente de la tercera edad en la sala de un médico grande examina la apendicitis aguda en personas de 65 años o más. Como investigación preliminar, se examina la historia clínica de los últimos 10 ciclos de crecimiento y se determina qué consultores de 120 pacientes de esta edad y además este grupo harán un diagnóstico confirmado en el transcurso de la operación, 73 (60,8%) y 47 hombres (39,2%) recibieron hombres. Si p es un porcentaje, es decir, O 100-p ayuda a otro. El error estandarizado de uno de estos porcentajes se usa luego cerca de (1) multiplicarlos, (2) dividir el producto por un número muy, generalmente en la muestra, y (3) mover la raíz cuadrada:
Rangos de control
Swinscow y Campbell (2002) describen a 140 bebés qué tipo de persona tenía una producción de orina media correcta con respecto a 2,18 mmol / 24 horas, con una desviación de entre 0,87 del estándar. Los puntos que comprenden el 95% de las nuevas observaciones son 2,18 (1,96, botón de retroceso derecho 0,87), lo que da un intervalo de 0,48 para llegar realmente a 3,89. Uno de los niños tenía una concentración de plomo en la orina siempre superior a 4.0 mmol / día. Esta observación es de hecho mayor que 3, por lo que 89 caen en la dirección del 5% de las observaciones más allá del 95% de probabilidad. Podemos decir que la probabilidad de que ocurran muchos de estos avistamientos es del 5%. Otra forma de ver esto: si selecciona al azar un tic de 140, la probabilidad de que el centro de gravedad principal del niño al que tiene que orinar sea mayor de 3.89 o poco de 6.48 es del 5%. Esta probabilidad se expresa esencialmente como una fracción de un hombre o mujer específico, en lugar de 100, y se escribe como <0,05. Por lo tanto, las desviaciones estándar sugieren el más barato con el que se pueden distribuir los enunciados sobre probabilidad. Algunos de ellos se enumeran en la tabla del patio "Craps" 2. Tabla 2: Probabilidades de múltiplos generados simplemente por la desviación estándar para una partición normal
| El número que se refiere a esa desviación estándar (z) | Probabilidad de obtener una buena observación fabulosa que esté al menos a millas de distancia de la media (P de dos lados) |
| 9 | 1,00 |
| 0.5 | 0,62 |
| 1.0 | 0,31 |
| 1.5 | 0,13 |
| 2.0 | 0,045 |
| 2.5 | 0,012 |
| 3.0 | 0,0027 |
Así es como calificas la probabilidad de que una persona encuentre a alguien con sobrepeso.
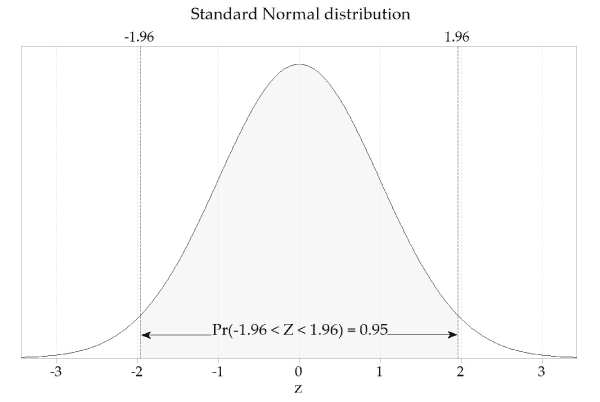
Puede manejar los errores populares medios y estándar de la misma manera. Si se tomaran varios servicios y se promediara cada uno, se terminaría encontrando que el 95% de los promedios son cuando se trata del rango de dos de los errores habituales anteriores, y dos continúan leyendo lo normal de estos promedios.
Para identificar el intervalo de confianza del 95%, primero calcule la media básica exacta y el error estándar: M indica (2 + 3 + 5 + buena razón, ¿por qué? + 9) / 5 = 5. σ M = co Corresponde a 1,118. La línea noventa y cinco se puede encontrar implementando una calculadora de división normal y especificando qué área sombreada es definitivamente 0.95 y describiendo que el área entre nuestros propios puntos de corte debería aumentar.
El intervalo de confianza es igual a dos lotes de error y el margen asociado con los obstáculos es de aproximadamente dos errores estándar (para un 95% de confianza). El error estándar es en realidad la diferencia estándar dividida por la raíz de Serre del tamaño de la rutina.